|
|
Post by Admin on May 19, 2023 16:00:21 GMT
Mondo
What you need to say is as follows:
We use (11) to write
$\mathcal{R}^{\phi}_q\circ\mathcal{R}^{\theta}_p=\mathcal{R}^{\psi}_r$
In words this means:
If we rotate the sphere through an angle $\theta$ about its axis through $p$, and then rotate the sphere through an angle $\phi$ about its axis through $q$, we obtain the same result that we would have obtained if instead we had rotated the sphere through an angle $\psi$ about its axis through $r$.
But having chosen the angles $\theta$ and $\phi$, what is the resultant angle of rotation about its axis through $r$?
We use the white triangle in 10a where the three angles add up to $kA(T)$, and so we can write
$($Angle sum of white triangle$)-\pi=kA(T)$
Since Angle sum of white triangle=$\theta/2+\phi/2+(\pi-\psi/2)$, we can write
$\theta/2+\phi/2+(\pi-\psi/2)-\pi=kA(T)$ and so
$\psi=\theta+\psi-2kA(T)$
Now we can see that the combined effect of the two rotations about $\theta$ and $\phi$ is a single rotation of $\psi=\theta+\psi-2kA(T)$ about the axis through $r$.
Vasco
|
|
|
|
Post by mondo on May 19, 2023 19:27:53 GMT
Mondo What you need to say is as follows: We use (11) to write $\mathcal{R}^{\phi}_q\circ\mathcal{R}^{\theta}_p=\mathcal{R}^{\psi}_r$ In words this means: If we rotate the sphere through an angle $\theta$ about its axis through $p$, and then rotate the sphere through an angle $\phi$ about its axis through $q$, we obtain the same result that we would have obtained if instead we had rotated the sphere through an angle $\psi$ about its axis through $r$. But having chosen the angles $\theta$ and $\phi$, what is the resultant angle of rotation about its axis through $r$? We use the white triangle in 10a where the three angles add up to $kA(T)$, and so we can write $($Angle sum of white triangle$)-\pi=kA(T)$ Since Angle sum of white triangle=$\theta/2+\phi/2+(\pi-\psi/2)$, we can write $\theta/2+\phi/2+(\pi-\psi/2)-\pi=kA(T)$ and so $\psi=\theta+\psi-2kA(T)$ Now we can see that the combined effect of the two rotations about $\theta$ and $\phi$ is a single rotation of $\psi=\theta+\psi-2kA(T)$ about the axis through $r$. Vasco Thank you Vasco, that's a really good, detailed answer. However, I have a few more questions: 1. You got a different result than it is in the book - $\psi=\theta+\psi-2kA(T)$ in your calculation vs $\psi=\theta+\psi-kA(T)$. Do you suggest a mistake in the book? 2. I am a bit questioning this equation from page 38 (let's focus on 2D case for now as it is simpler) $(R_{L_2'} \cdot R_{L_1'}) \cdot (R_{L_2} \cdot R_{L_1}) = R_{L_2'} \cdot R_{L_1}$. I question it from the equality perspective - to me it looks like the left hand side rotates about completely different point than the right hand side of this equation and hence the net rotation of figures on a plane cannot be equal. Here is my simple sketch to prove that (sorry for the quality, this is accuracy of MS paint) 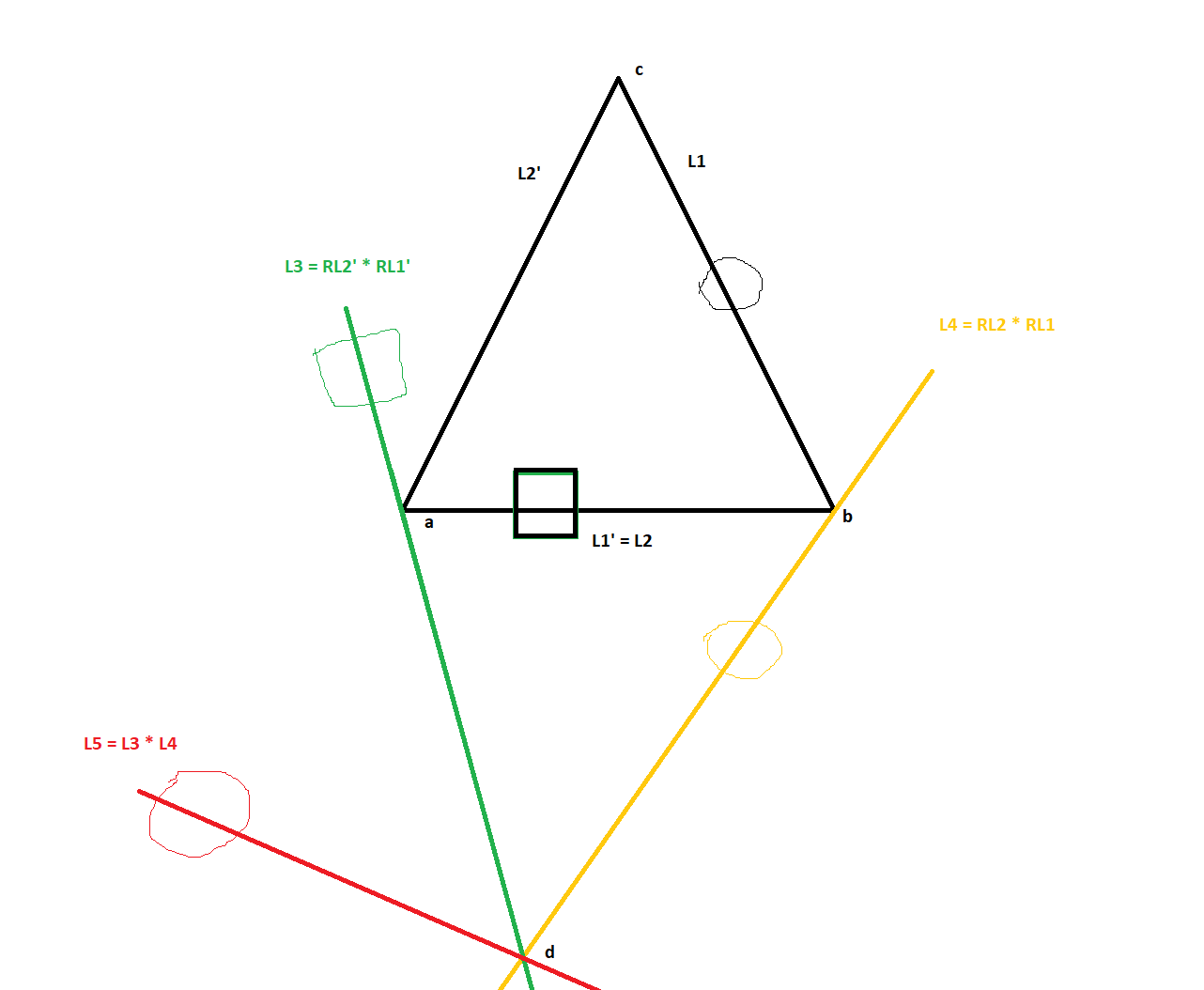 So at the beginning we only had the black equilateral triangle, then I made a series of rotations: 1. Rotation of $L2' \cdot L1'$ - this rotated the line through points $a,b$ into the green line which I called $L3$. Also note the black rectangle on the black line was rotated to the green one on $L3$ . 2. Another rotation this time $L2 \cdot L1$ which generated an orange color line called $L4$. Note how the manually drawn black circle from line through points $b,c$ is now on the orange line. 3. Final rotation of $L3 \cdot L4$ - this generates a red line called $L5$. The manually drawn circle is rotated again (I did not draw another rectangle rotation to not obfuscate the drawing). So now we see how the circle traveled with the sequence of rotations. The big question now is where would it be if I had simply done $RL1 \cdot L2'$ instead? It is not hard to imagine that it would end up in a completely different location. Probably the angle in respect to the line through $a,b$ would be the same but definitely these two circles would not overlap - there would be an offset. That said, can we call these two rotations here $(R_{L_2'} \cdot R_{L_1'}) \cdot (R_{L_2} \cdot R_{L_1}) = R_{L_2'} \cdot R_{L_1}$ are "equal"? Thank you. |
|
|
|
Post by Admin on May 19, 2023 19:52:14 GMT
Mondo
Which printing of the book do you have? Looks like you may have an early version which contains errors which are corrected in later versions.
On page 282 in my book the 2 is present.
On page 38 those Rs do not refer to rotations but to reflections. That's why they are in a different font.
Vasco
|
|
|
|
Post by mondo on May 19, 2023 19:58:09 GMT
Mondo Which printing of the book do you have? Looks like you may have an early version which contains errors which are corrected in later versions. On page 282 in my book the 2 is present. My version is 2000 reprint (with corrections). On page 38 those Rs do not refer to rotations but to reflections. That's why they are in a different font. Ok, but my question is still valid right? These two rotation from left/right hand side of equation are not the same. Meaning if you rotate using left hand side method you will not get the plane in the same location as if you had done it via right hand side of this equation on page 38. |
|
|
|
Post by Admin on May 19, 2023 20:05:04 GMT
Mondo
Hang on! On page 282 the equation contains a 2 in the equation. Why are you saying it doesn't?
Vasco
|
|
|
|
Post by Admin on May 19, 2023 20:10:30 GMT
Mondo
How can your question be still valid when we are talking reflections and not rotations?
Vasco
|
|
|
|
Post by mondo on May 19, 2023 20:24:24 GMT
Mondo Hang on! On page 282 the equation contains a 2 in the equation. Why are you saying it doesn't? Vasco Here is what is printed in my book:  How can your question be still valid when we are talking reflections and not rotations? I just looked at page 38 again and it clearly talks about a rotation, last paragraph of page 38 - "For example, see [30a]. Here a rotation about a thrugh $\theta$ is being represented as $R_{L_2} \cdot R_{L_{1}}..$" So why do you say it is a reflection? |
|
|
|
Post by Admin on May 19, 2023 20:52:02 GMT
Mondo
That equation on page 282 of your book is incorrect. Later prints of the book have the correct version.
I see what you mean: the rotations are achieved by 2 reflections, but note that the lines $L_2$ and $L'_1$ are coincident. (see the last paragraph on page 38).
Vasco
|
|
|
|
Post by mondo on May 19, 2023 21:07:36 GMT
That equation on page 282 of your book is incorrect. Later prints of the book have the correct version. Ok, makes sense - I agree with your calculations. Will make a note on a side of my book. I see what you mean: the rotations are achieved by 2 reflections, but note that the lines $L_2$ and $L'_1$ are coincident. (see the last paragraph on page 38). I know that they are coincidental, that's how we got a triangle. I think I may have a mistake in my paint drawing, I have to go thru it again. What I try to get is the net rotation thru point $c$ is the same as if we had done it in steps of left hand side equation. Thanks for the suggestions! |
|
|
|
Post by Admin on May 19, 2023 21:18:47 GMT
Mondo
No problem. Let me know if you have any more questions
Vasco
|
|
|
|
Post by Admin on May 20, 2023 8:10:20 GMT
Mondo
In your post #31 you have the equation on page 38:
$(\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L'_1})\circ(\mathfrak{R}_{L_2}\circ\mathfrak{R}_{L_1})=\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L_1}$
The reason the left hand side is equal to the right hand side is because if we write the left hand side as
$\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L'_1}\circ\mathfrak{R}_{L_2}\circ\mathfrak{R}_{L_1}$
and note that
$\mathfrak{R}_{L'_1}\circ\mathfrak{R}_{L_2}$ is an identity transformation if $L'_1$ and $L_2$ are the same line,
then the left hand side becomes
$\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L_1}$, which is the right hand side of the original equation.
Vasco
|
|
|
|
Post by mondo on May 20, 2023 18:54:49 GMT
Mondo In your post #31 you have the equation on page 38: $(\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L'_1})\circ(\mathfrak{R}_{L_2}\circ\mathfrak{R}_{L_1})=\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L_1}$ The reason the left hand side is equal to the right hand side is because if we write the left hand side as $\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L'_1}\circ\mathfrak{R}_{L_2}\circ\mathfrak{R}_{L_1}$ and note that $\mathfrak{R}_{L'_1}\circ\mathfrak{R}_{L_2}$ is an identity transformation if $L'_1$ and $L_2$ are the same line, then the left hand side becomes $\mathfrak{R}_{L'_2}\circ\mathfrak{R}_{L_1}$, which is the right hand side of the original equation. Vasco Vasco, yes that makes perfect sense. I got confused because I was trying to prove it in a sequence of rotations $R_{L_2'} \circ R_{L_1'}$ and then $R_{L_2} \circ R_{L_1}$ but the problem is after the first rotation is done, what is the rotation (pivot) point now? Did it move as part of the previous rotation (it should)? |
|