|
|
Post by Admin on Jul 13, 2023 5:54:31 GMT
Mondo
The graph looks correct after I added some + signs which are missing.
I'll have to check the maths.
Vasco
|
|
|
|
Post by mondo on Jul 13, 2023 6:04:40 GMT
Mondo The graph looks correct after I added some + signs which are missing. I'll have to check the maths. Vasco Thank you. This is how the graph looks like on my end 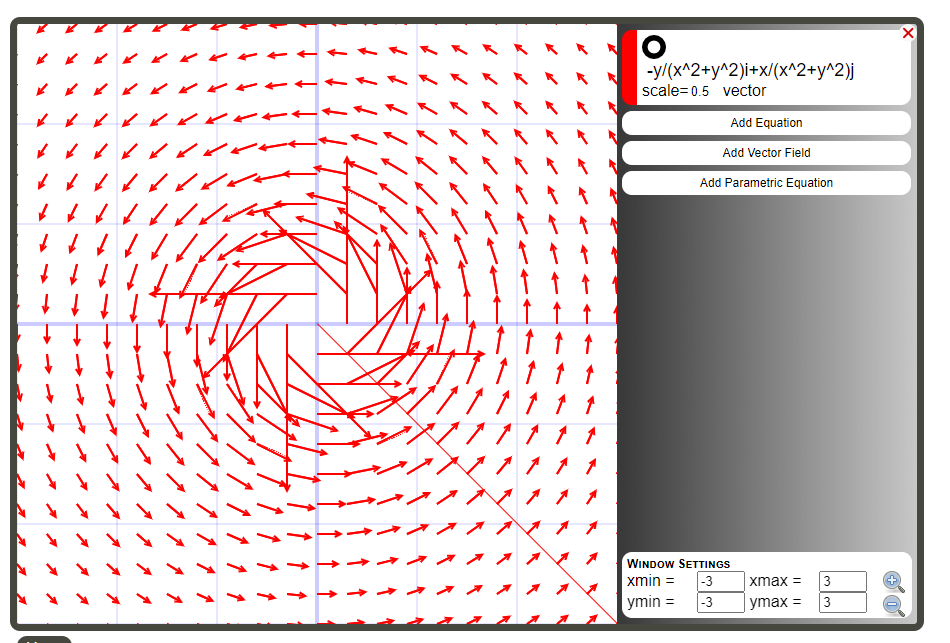 |
|
|
|
Post by Admin on Jul 13, 2023 6:25:46 GMT
Mondo
Thanks. Yes the link works fine now.
Vasco
|
|
|
|
Post by mondo on Jul 13, 2023 7:03:44 GMT
Ok.
I try to conclude this thread, it looks like we can calculate work/flux in two ways. One is to do the contour integration (this is what you did in your supplement document). It is also the quickest, intuitive way, as you can visualize say work as multiplication of total path length times tangent component to this path. The second way is to use the curl, which requires a double integral over the region bounded by our loop. Do you agree with this Vasco?
Additionally, just on the next page I found a sentence that doesn't make sense to me(second to last paragraph of page 489) "Rotating the picture of $\overline{z}$ through $\pi/2$ clearly yields the negative of the original field, and correspondingly negative of the work and flux." How does the rotation by $90\deg$ makes the vector field negative? How can it return negative work? If say work was vanishing previously, then an equal rotation of entire image should not change the work a bit right?
Thank you.
|
|
|
|
Post by Admin on Jul 13, 2023 9:26:12 GMT
Mondo
Yes I agree with what you say in the first part.
As for the second part, you have missed the point the author is making:
We can see from the left hand side of figure 13 on page 490 that if we rotate the figure the vector field will change sign which would mean that the work and flux would change sign too. But since they must remain unchanged by the rotation, then the only way this would be possible is for them both to vanish, as Needham says. So it's a way of showing that $W$ and $F$ must vanish.
Vasco
|
|
|
|
Post by mondo on Jul 13, 2023 20:42:19 GMT
But a rotation of $\pi/2$ doesn't change the sign of the vector field right? A rotation of $\pi$ would change it though. For instance, if we take the vector field arrows on the left hand side of figure [13] and rotate them by $\pi/2$ the ones that pointed in positive $X$ axis now point in positive $Y$ axis. Also, $\overline{z} = x - iy$, a rotation by $\pi/2$ means a multiplication by $i$ hence we have $i\overline{z} = y + ix$ so where does it "Yield a negative of the original field"?
|
|
|
|
Post by Admin on Jul 13, 2023 21:47:50 GMT
Mondo
If we rotate the left hand side diagram 13 through $\pi/2$, then the arrows anchored on the right hand side of the circle and pointing outside the circle before the rotation would now be anchored on the top of the circle, pointing outside the circle. So they would be pointing in exactly the opposite direction to the ones at the top of the circle before the rotation, which are pointing inside the circle.
So the direction of the field has been reversed or in other words is the negative of what it was before.
Vasco
|
|
|
|
Post by mondo on Jul 13, 2023 22:22:46 GMT
Ahh right right right! I should have guessed that.. thank you Vasco!
|
|