|
|
Post by mondo on Sept 4, 2022 18:09:32 GMT
Hello, in the subsection 3 "The geometry of the Mapping" author is urging to sketch mappings like $z$ -> $\frac{1}{2}e^{z}$ or $z$ -> $\cos(z)$. Is there any online graph tool that can do that? I tried with equation explorer but it doesn't work Equation Explorer. Looks like it is tuned for vector fields. A hand drawing is difficult here as you need to know what $z$ to pick to make the graph reasonable. Thank you. |
|
|
|
Post by Admin on Sept 4, 2022 19:09:47 GMT
Hello, in the subsection 3 "The geometry of the Mapping" author is urging to sketch mappings like $z$ -> $\frac{1}{2}e^{z}$ or $z$ -> $\cos(z)$. Is there any online graph tool that can do that? I tried with equation explorer but it doesn't work Equation Explorer. Looks like it is tuned for vector fields. A hand drawing is difficult here as you need to know what $z$ to pick to make the graph reasonable. Thank you. Mondo A hand drawing is not that difficult and you will really understand what you have done. If you do it by computer you won't understand it. Make sure you can draw figure 26 on page 88 by hand from the equations before you try the suggested exercises. Once you can draw 26 you will be able to draw almost anything. Get some graph paper. You might need a calculator for sines and cosines and some simple arithmetic. You might find it useful to know that $\sin(\pi/6)=\cos(\pi/3)=(1/2)$ $\sin(\pi/3)=\cos(\pi/6)=(\sqrt{3}/2)$ $\sin(\pi/4)=\cos(\pi/4)=(\sqrt{2}/2)$ Maybe you already know this. If you get stuck ask. Vasco |
|
|
|
Post by Admin on Sept 4, 2022 19:22:35 GMT
Mondo
If you look in useful links you will find some graphics software but it doesn't do complex arithmetic.
Vasco
|
|
|
|
Post by Admin on Sept 4, 2022 21:42:58 GMT
Mondo
You could use Desmos software to do this but you would have to break everything down into real and imaginary parts to plot it.
I would advise doing a sketch by hand and then check it with Desmos.
Vasco
|
|
|
|
Post by mondo on Sept 5, 2022 6:26:24 GMT
A hand drawing is not that difficult and you will really understand what you have done. If you do it by computer you won't understand it. Make sure you can draw figure 26 on page 88 by hand from the equations before you try the suggested exercises. Yes this is the figure that I try to reproduce. I agree, doing it by hand has the most learning value. Once you can draw 26 you will be able to draw almost anything. Get some graph paper. You might need a calculator for sines and cosines and some simple arithmetic. So I started with $\frac{1}{2}e^z$. Figure 26 actually does this mapping to $iz$ hence $\frac{1}{2} e^{iz} = \frac{1}{2} e^{c + it} = \frac{1}{2} e^c cos(t) + e^c sin(t)$ Having the formula I set $c = 2; t = [-5..5]$ and got points that resemble a circle. I think this exercise is done. I don't think there is any quicker way to get the feel of how this image $e^{iz}$ of $z$ looks like? Next I am going to draw $\cos(z)$, will be back with an update. You might find it useful to know that $\sin(\pi/6)=\cos(\pi/3)=(1/2)$ $\sin(\pi/3)=\cos(\pi/6)=(\sqrt{3}/2)$ $\sin(\pi/4)=\cos(\pi/4)=(\sqrt{2}/2)$ Maybe you already know this. To be honest I never remember it, unless I used it yesterday. But it is very easy to get, every pocket calculator has these ones built in. Thank you. |
|
|
|
Post by Admin on Sept 5, 2022 6:36:42 GMT
Mondo
Should be $\frac{1}{2} e^{iz} = \frac{1}{2} e^{c + it} = \frac{1}{2} [e^c cos(t) + ie^c sin(t)]=\frac{1}{2} e^c [cos(t) + isin(t)]$
You missed out the i and some brackets.
You say you got something which resembles a circle. But that's not good enough. It should be an exact circle.
So what two quantities did you plot to get something which resembles a circle? What was the radius of the circle? Measure it with a ruler.
What should the radius be do you reckon? What did yours measure? Was it what it should be?
Vasco
|
|
|
|
Post by Admin on Sept 7, 2022 21:14:47 GMT
Mondo
How are you getting on with your sketching/drawing of the curves?
Vasco
|
|
|
|
Post by mondo on Sept 8, 2022 8:01:00 GMT
Hello Vasco, I will do my best to get back into this today.. got caught up by some other work  PS: Thanks for motivating  |
|
|
|
Post by mondo on Sept 8, 2022 20:12:22 GMT
Mondo Should be $\frac{1}{2} e^{iz} = \frac{1}{2} e^{c + it} = \frac{1}{2} [e^c cos(t) + ie^c sin(t)]=\frac{1}{2} e^c [cos(t) + isin(t)]$ You missed out the i and some brackets. Yes, I missed it here as I was responding quite late, in my notebook I have it right. Thanks for spotting. You say you got something which resembles a circle. But that's not good enough. It should be an exact circle. I said resembles because on a piece of paper I just did 10 points for t[-5..5] and it indeed was forming a circular shape. However for a better accuracy I employed some software and: - defined an array $t$ from $-1000$ to $1000$ - defined constant $c = 2$ - calculated real component $x = 0.5e^{c}[cos(t)]$ - calculated imaginary component $y = 0.5e^{c}[sin(t)]$ And finally plotted X versus Y. Here is what I am getting: 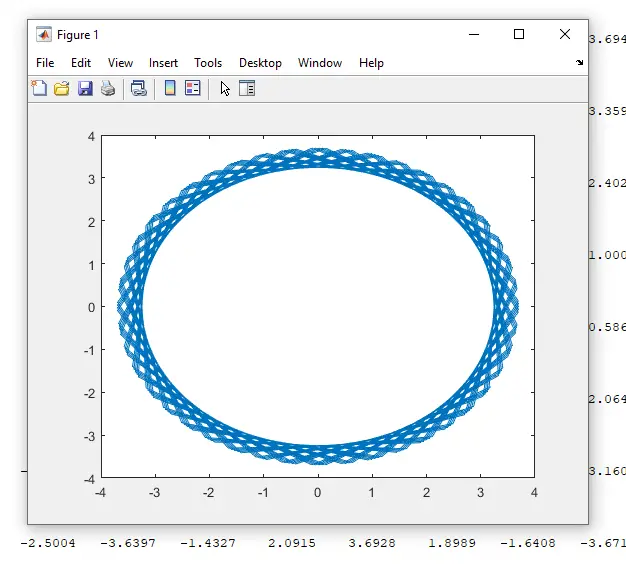 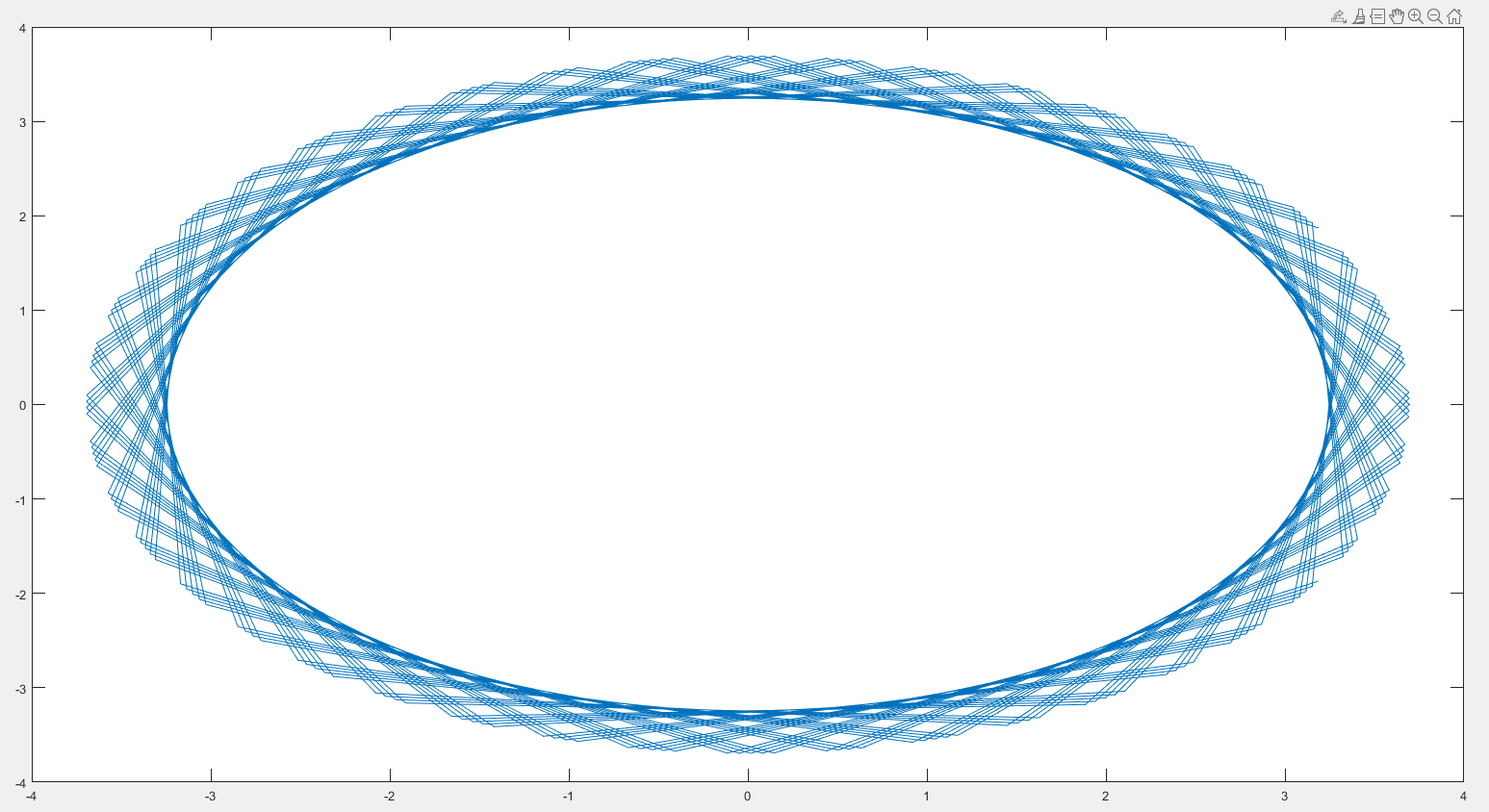 What was the radius of the circle? Measure it with a ruler. Good question, the radius we are looking for is $r = \frac{1}{2}e^2 = 3.69$. On paper I am getting exactly that. In the software, well not quite...the boundary is fuzzy and the radius seems to closer to $3$. The second image looks oval but this is because of zoom - by the scale from $-4$ to $4$ it should be circle. |
|
|
|
Post by mondo on Sept 8, 2022 22:05:38 GMT
This is what happens if I restrict $t$ to be in a range from $-\pi$ to $\pi$  which is what we want. So looks like I was facing "a rounding" error of $\cos()$ function when the argument is outside its normal interval $=-\pi \le x \le \pi$? |
|
|
|
Post by mondo on Sept 8, 2022 23:57:18 GMT
For the mapping $z$ -> $cos(z) = cos(t-ic)$ I have even more fundamental problem, namely how to get $x,y$ formulas. I try by $\cos(t-ic) = cos(t)cos(ic) + sin(t)sin(ic)$, now how to factor $x,y$ components if both contain $i$?
If I use the identity $cos(z) = \frac{e^{iz} + e^{-iz}}{2}$, expand it using Euler formula (as in the previous example) then the imaginary part vanish as I will have two $\sin()$ function with opposite sign.
Also, "The image under $\cos(z) $ .. is the sum of these counter-rotating circular motions" I don't get that. What "Counter-rotating motions" are assumed here?
|
|
|
|
Post by Admin on Sept 9, 2022 15:28:55 GMT
Mondo
In reply to your post #8 above I don't see how those very strange plots can be caused by rounding. There must be something wrong with the way you calculated them. Try plotting the circle with double the range above i.e. -$2\pi$ to $+2\pi$ and see what happens.
The fact that it is an ellipse is as you say because the scale is different in the $x$ and $y$ directions. What is the plotting software you are using?
In the first two plots it's the external shape which agrees with the maths not the internal shape. It would be good if you could set the scale to be the same along both axes and so get a circle.
Vasco
|
|
|
|
Post by Admin on Sept 9, 2022 15:45:05 GMT
For the mapping $z$ -> $cos(z) = cos(t-ic)$ I have even more fundamental problem, namely how to get $x,y$ formulas. I try by $\cos(t-ic) = cos(t)cos(ic) + sin(t)sin(ic)$, now how to factor $x,y$ components if both contain $i$? you would need to substitute for $\cos(ic)$ and $\sin(ic)$ See pages 86-87. But all this algebra is already done for you on page 88. You need to read and really understand page 88 to do this. yes but they are multiplied by different factors and so do not cancel out. Look at the diagram and you see the two circles with a particle rotating round each. Again make sure you understand everything on page 88. All the maths is done for you on this page so that you can plot the ellipses Vasco |
|
|
|
Post by Admin on Sept 10, 2022 7:03:03 GMT
Mondo
In my reply 12 above I misunderstood what you meant and so my answer was incorrect about the cancelling of the sine terms in the expansion of $0.5(e^{iz}+e^{-iz})$. Sorry about that.
But note the warning in the middle of page 85 regarding $e^{iz}$.
It's better to write
$0.5(e^{iz}+e^{-iz})=0.5(e^ce^{it}+e^{-c}e^{-it})$.
This is what I meant. Because if you now expand $e^{it}$ and $e^{-it}$ you will see that the sine terms do not cancel out, except in the special case when $c=0$ and $z$ is real and we get the real function $\cos$.
Vasco
|
|
|
|
Post by mondo on Sept 10, 2022 16:59:48 GMT
In reply to your post #8 above I don't see how those very strange plots can be caused by rounding. There must be something wrong with the way you calculated them. Try plotting the circle with double the range above i.e. -$2\pi$ to $+2\pi$ and see what happens. In fact it is not the range that matters here but rather a step. If I define $t [-100:1:100]$ which means from $-100$ to $100$ with a step equal $1$ then I am getting that weird plot. However if I change the step from $1$ to $\frac{\pi}{10}$ all is fine and I get a normal circle. NOTE, it must be a fraction of $\pi$ otherwise I am getting a straight line with negative slope. There is one more way to get a smooth circle from $t [-100:1:100]$ - change $\cos()$ function to $cosd()$ which argument is supposed to be in degrees not radians. So I think my initial suspicion about rounding error was correct. Just matlabs $\cos$ function expect argument in radians and I was feeding it with integer multiples. The fact that it is an ellipse is as you say because the scale is different in the $x$ and $y$ directions. What is the plotting software you are using? In the first two plots it's the external shape which agrees with the maths not the internal shape. It would be good if you could set the scale to be the same along both axes and so get a circle. I am using MATLAB here. If you have access to it I can share my script. It's better to write $0.5(e^{iz}+e^{-iz})=0.5(e^ce^{it}+e^{-c}e^{-it})$. This is what I meant. Because if you now expand $e^{it}$ and $e^{-it}$ you will see that the sine terms do not cancel out, except in the special case when $c=0$ and $z$ is real and we get the real function $\cos$. Yes I overlooked the different exponent. So now I have $0.5(e^{c}e^{it} + e^{-c}e^{-it}) = 0.5(e^{c}\cos(t) + e^-c\cos(t) + e^{c}i\sin(t) - e^{-c}i\sin(t))$ Now separating real and imaginary parts I again plotted it hoping to see a nice oval as in the book. However what I get is very close to the circle from $0.5e^z$ example. To make it more visible I plotted them together. (The red one is supposed to be oval. 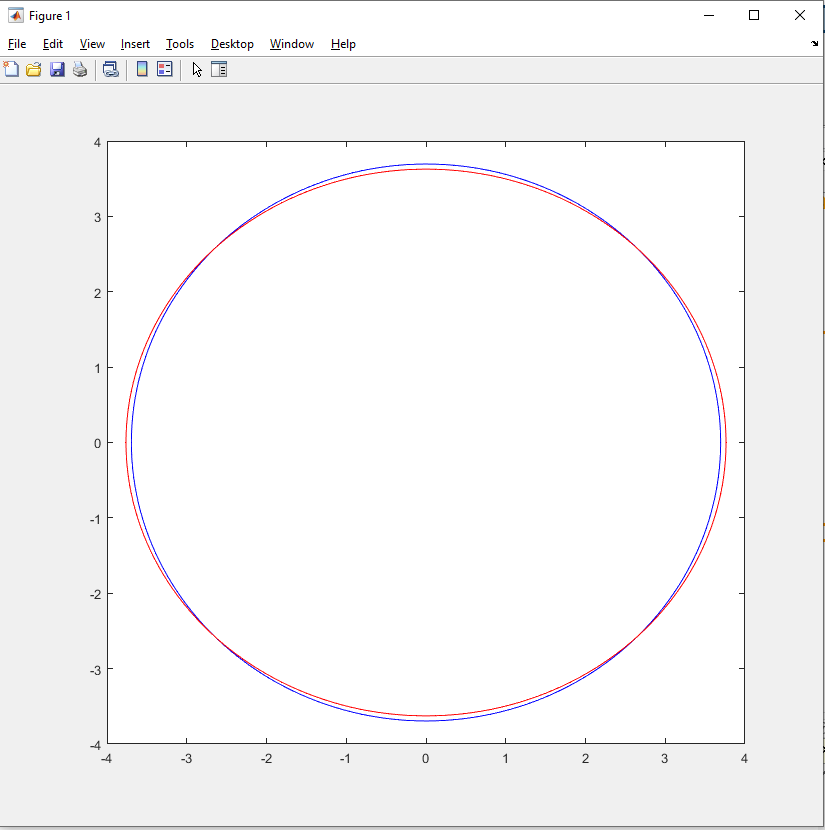 |
|