|
|
Post by mondo on Jun 11, 2023 22:31:10 GMT
I have problems understanding this material. The very first equation, (1) in this chapter on page 427 is given as an axiom and this makes it much more difficult to understand almost every other equation in this chapter as they all rely on the first one. For instance, on page 431, I don't understand why $f'(a) = \frac{1}{2\pi i} \int_L \frac{F_a(z)}{z-a}dz$? Why the derivative is equal to an integral?
|
|
|
|
Post by Admin on Jun 11, 2023 23:23:12 GMT
Mondo
Can you please check that the page numbers are correct? Thanks
Vasco
|
|
|
|
Post by mondo on Jun 11, 2023 23:41:56 GMT
The first one was wrong 427 instead of 417, a typo. Corrected.
|
|
|
|
Post by Admin on Jun 12, 2023 6:22:24 GMT
I have problems understanding this material. The very first equation, (1) in this chapter on page 427 is given as an axiom and this makes it much more difficult to understand almost every other equation in this chapter as they all rely on the first one. For instance, on page 431, I don't understand why $f'(a) = \frac{1}{2\pi i} \int_L \frac{F_a(z)}{z-a}dz$? Why the derivative is equal to an integral? Mondo Equation (1) on page 427 is not presented as an axiom. Needham gives two explanations of it. Vasco |
|
|
|
Post by Admin on Jun 12, 2023 6:50:23 GMT
Mondo
I will get back to you about the equation on page 431.
Vasco
|
|
|
|
Post by Admin on Jun 12, 2023 13:57:42 GMT
I have problems understanding this material. The very first equation, (1) in this chapter on page 427 is given as an axiom and this makes it much more difficult to understand almost every other equation in this chapter as they all rely on the first one. For instance, on page 431, I don't understand why $f'(a) = \frac{1}{2\pi i} \int_L \frac{F_a(z)}{z-a}dz$? Why the derivative is equal to an integral? Mondo This is all explained in section I of chapter 9 on pages 427-431. What is it specifically about this expression that you do not understand? Vasco |
|
|
|
Post by Admin on Jun 14, 2023 6:23:46 GMT
Mondo
I forgot to point out to you that the integral is a loop integral and so should be written as
$\displaystyle f'(a)=\frac{1}{2\pi i}\oint_L\frac{F_a(z)}{z-a}dz$
Vasco
|
|
|
|
Post by mondo on Jun 15, 2023 6:29:36 GMT
Vasco, thank you. I reread this chapter + used your suggestions and I think I understand a lot more now. At first I got confused by the fact that we integrate an amplitwist function $F(a)$ in the integrals like the last on page 430. But it looks like author just uses this as a mean to show "infinite differentiability" of analytic functions.
At this point I have one question related to Taylor vs Laurent series - it appears to me the later is more "generic". What I mean by that is in Taylor series we start expanding from power $0$ to some $n$th power, in Lauren series on the other hand we expand from $-m$th to 0 and then continue to $m$. So it looks like with Laurent series we can represent a function without a singularity just as good as a taylor series right?
|
|
|
|
Post by Admin on Jun 15, 2023 19:03:32 GMT
Vasco, thank you. I reread this chapter + used your suggestions and I think I understand a lot more now. At first I got confused by the fact that we integrate an amplitwist function $F(a)$ in the integrals like the last on page 430. But it looks like author just uses this as a mean to show "infinite differentiability" of analytic functions. At this point I have one question related to Taylor vs Laurent series - it appears to me the later is more "generic". What I mean by that is in Taylor series we start expanding from power $0$ to some $n$th power, in Lauren series on the other hand we expand from $-m$th to 0 and then continue to $m$. So it looks like with Laurent series we can represent a function without a singularity just as good as a Taylor series right? Mondo I agree that the Laurent series is more general than the Taylor series. Vasco |
|
|
|
Post by mondo on Jun 26, 2023 2:41:44 GMT
On page 428 below figure [1] author says "In the previous chapter we saw geometrically that if $\theta$ increases by $d\theta$, causing $z_0$ to move $dz$ along the circle, then $\frac{dz}{(z-a)} = id\theta$." - I draw a helper diagram but I still can't see why is it true, I also don't recall such a relation from a previous chapters. Do you understand it Vasco?
Even if we write it down: $\frac{dz}{(z-a)} = \frac{izd\theta}{(z-a)} \ne id\theta$ it doesn't make sense.
Thank you.
|
|
|
|
Post by Admin on Jun 26, 2023 19:41:55 GMT
Mondo
This is almost exactly the same as figure 4 on page 437 except that the circle is not the unit circle, but a general circle centred at $a$.
Vasco
|
|
|
|
Post by mondo on Jun 26, 2023 21:41:34 GMT
Mondo This is almost exactly the same as figure 4 on page 437 except that the circle is not the unit circle, but a general circle centred at $a$. Vasco Yes I see the similarity but still, even if we write it down: $\frac{dz}{(z-a)} = \frac{izd\theta}{(z-a)} \ne id\theta$. In order for the last equation to be true we would have to have $(z-a)$ instead of $z$ in the numerator but we don't. We just rotate $z$ which is independent of a circle rotation right? |
|
|
|
Post by Admin on Jun 26, 2023 22:53:09 GMT
Mondo
I disagree with you. It looks perfectly correct to me.
Vasco
|
|
|
|
Post by Admin on Jun 26, 2023 23:02:31 GMT
Mondo
We have a circle of radius $r$ centred at $a$ and so $z=a+re^{i\theta}$ and therefore $dz=ire^{i\theta}d\theta=i(z-a)d\theta$
So $\displaystyle\frac{dz}{z-a}=id\theta$
Vasco
|
|
|
|
Post by mondo on Jun 26, 2023 23:20:54 GMT
Mondo We have a circle of radius $r$ centred at $a$ and so $z=a+re^{i\theta}$ and therefore $dz=ire^{i\theta}d\theta=i(z-a)d\theta$ So $\displaystyle\frac{dz}{z-a}=id\theta$ Vasco I see it this way 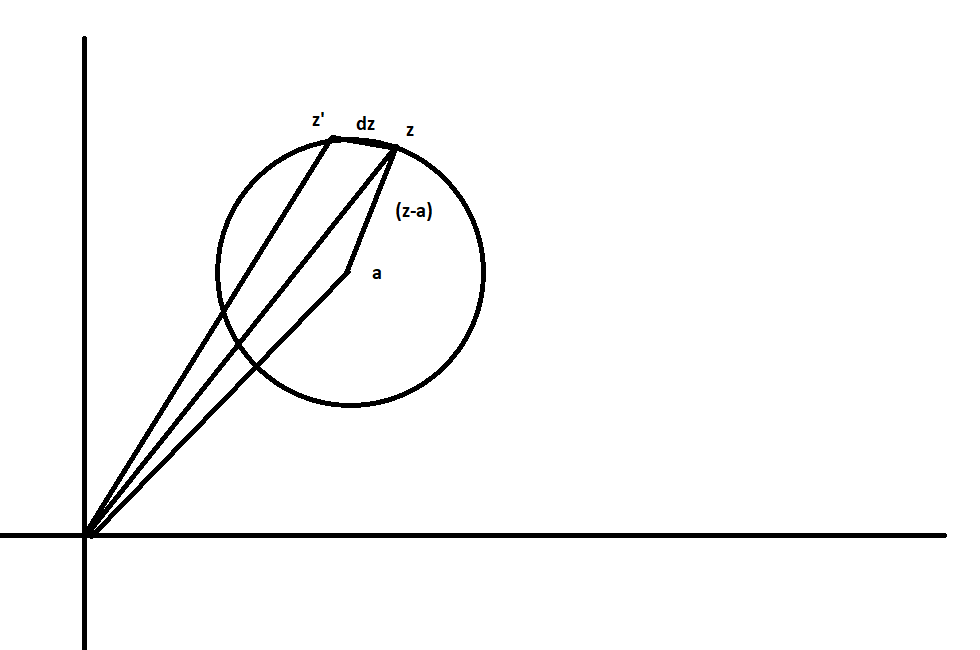 I have to think about it, I just couldn't make sense of these numbers in accord with the above figure. Like, division by (z-a) was meaningless on the figure. UPDATE: Ok, the problem is: I saw it as $z$ rotating around the circle, after all $dz$ is increment of $z$. But this cannot be true as then $z$ would have to change it's length during its journey around $C_r$. So, what really rotates around this circle is not $z$ but $(z-a)$ and hence to be strict we should call the increment vector $d_{(z-a)}$ or something like $dza$ or $dc$ where $c=(z-a)$. Anyway, thank you Vasco for explaining, I see it now! |
|