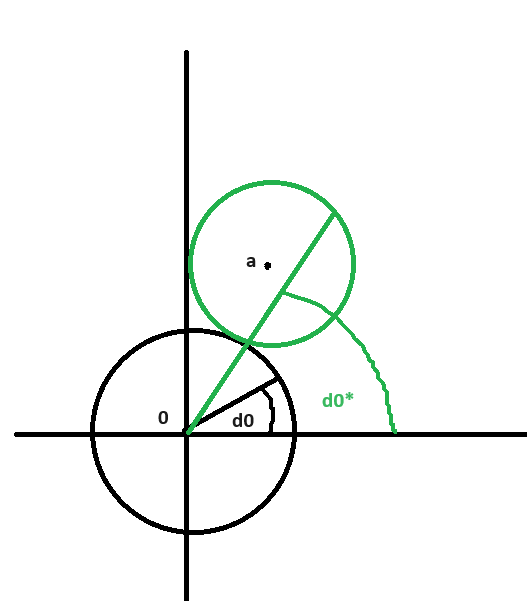|
|
Post by mondo on Sept 24, 2023 6:25:28 GMT
So far I stumbled on several places in this subchapter that are not clear to me: 1 p.555, equation (28). Here I wonder why do we care where the circle is centered/located - all we need it to take the average over its circumference. Hence even if the circle is centered at some $a$ we can just pretend it is at $0$ and calculate average of its values. This should be the same regardless of circle location. 2. For the same equation, how was this generalized formula for $T(a)$ derived? Do you have any idea? 3. p.556, right below equation (30) author says "in which it should be stressed that the averaging is still taking place with respect to the angle of $z$, not its image z*". So we take values of the new temperature distribution but round a completely different circle? This does not make sense. This is how I see it:  i2.paste.pics/166dd1ad300bc5e74f909532f5d0f0b5.png i2.paste.pics/166dd1ad300bc5e74f909532f5d0f0b5.pngIf we use $d\theta$ to measure average temperature on the upper half of the circle (from $-\pi to \pi$) then we can see that since $d\theta*$ is leading $d\theta$ we won't sum all it's values by the time we complete the integration path with the other circle. 4. Equation (32) p.558, similarly as above I don't get this "re-expression" 5. p.559, second paragraph, "As an interesting consequence...the level curves of $P_a$ are the circles which are tangent to $C$", hmm why is that? 6. p.559, last equation, I understand the middle part of it but I don't see why is it $Re(\frac{z+a}{z-a})$? Thank you. |
|
|
|
Post by Admin on Sept 24, 2023 13:35:31 GMT
Mondo
1. $a$ is not the centre of the circle.
2. Read sentence immediately after (27). Proof follows in the following pages.
Vasco
|
|
|
|
Post by Admin on Sept 24, 2023 19:10:44 GMT
Mondo
6. I don't understand why you can't see this from figure 35.
Consider the two vectors represented by the arrows, one is $|z+a|e^{i\alpha}$ and the other is $|z-a|e^{i\beta}$, where $\alpha$ and $\beta$ are the arguments of the two vectors. Since from the diagram we can see that $\gamma=\alpha-\beta$ then:
$\displaystyle\text{Re}\bigg(\frac{z+a}{z-a}\bigg)=\text{Re}\bigg(\frac{|z+a|}{|z-a|}e^{i(\alpha-\beta)}\bigg)=\frac{|z+a|}{|z-a|}\cos\gamma$
Vasco
|
|
|
|
Post by Admin on Sept 24, 2023 19:24:29 GMT
Mondo
3. and 4. I would ask you to reread the explanation in the book, as it explains everything, and I do not want to write all that wonderful explanation again here.
Vasco
|
|
|
|
Post by Admin on Sept 24, 2023 19:34:49 GMT
Mondo
5. Use Desmos to draw the level curves of $\mathcal{P}_a(z)$ and you will see it.
Vasco
|
|
|
|
Post by mondo on Sept 24, 2023 20:58:08 GMT
Mondo 6. I don't understand why you can't see this from figure 35. Consider the two vectors represented by the arrows, one is $|z+a|e^{i\alpha}$ and the other is $|z-a|e^{i\beta}$, where $\alpha$ and $\beta$ are the arguments of the two vectors. Since from the diagram we can see that $\gamma=\alpha-\beta$ then: $\displaystyle\text{Re}\bigg(\frac{z+a}{z-a}\bigg)=\text{Re}\bigg(\frac{|z+a|}{|z-a|}e^{i(\alpha-\beta)}\bigg)=\frac{|z+a|}{|z-a|}\cos\gamma$ Vasco I think the easiest way to see it is - when vectors are collinear then operations on them are operation on theirs real parts. As for $\gamma=\alpha-\beta$ - how did you get that? If we look at [35] we can see when these two vectors are translated back to the origin then $\beta$ is much wider angle, then it should rather be $\gamma=\beta-\alpha$ ? |
|
|
|
Post by Admin on Sept 24, 2023 22:54:46 GMT
Mondo
What you are saying is in my opinion totally and utterly wrong. The fact that $\gamma=\alpha-\beta$ is staring you in the face when you look at figure 35.
Vasco
|
|
|
|
Post by mondo on Sept 24, 2023 23:53:27 GMT
Mondo What you are saying is in my opinion totally and utterly wrong. The fact that $\gamma=\alpha-\beta$ is staring you in the face when you look at figure 35. Vasco Hmm I don't see it really, help me here - $\alpha$ is an angle between what and what? They are not originating from $0$ so I am not sure you can say $p = |z-a|e^{i\beta}$ |
|
|
|
Post by mondo on Sept 25, 2023 0:14:01 GMT
Mondo 3. and 4. I would ask you to reread the explanation in the book, as it explains everything, and I do not want to write all that wonderful explanation again here. Vasco Yes I read the paragraph which follows, starting from "We may interpret (30) as.." but it still doesn't give me a clear answer. Is that because $\theta*$ will depend/be a fuction of $\theta$? But then this integral can not be evaluated as it stands since in (30) it reads as integral of a constant $T(\theta*)$ from $-\pi$ to $\pi$. |
|
|
|
Post by Admin on Sept 25, 2023 6:42:06 GMT
Mondo What you are saying is in my opinion totally and utterly wrong. The fact that $\gamma=\alpha-\beta$ is staring you in the face when you look at figure 35. Vasco Hmm I don't see it really, help me here - $\alpha$ is an angle between what and what? They are not originating from $0$ so I am not sure you can say $p = |z-a|e^{i\beta}$ Mondo $\alpha$ is the argument of the complex number (or vector) $z+a$. Look at page 97 and read subsection 4 from page 96-98. This is an example of using vectors as complex numbers without anchoring them at 0. Vasco |
|
|
|
Post by Admin on Sept 25, 2023 14:30:44 GMT
Mondo
$\alpha$ and $\beta$ are just used by me for the arguments of $z+a$ and $z-a$ in figure 35 to make it easier to see the result at the bottom of page 559. If we extend the line from $-z$ to $a$ then we can see that the angle between $z-a$ and $z+a$ is $\beta-\alpha=\gamma$.
You were right when you said it should be $\beta-\alpha$ not $\alpha-\beta$, but it doesn't affect the reasoning. We get the same result.
Vasco
|
|
|
|
Post by mondo on Sept 25, 2023 19:16:24 GMT
Ok, and you were right when you said the angle is staring at you - no matter where the vectors are in the plane (not starting from the origin) the angle between them is always the same. So in this case, no calculation is needed to see it is $\gamma$. But what abut the real part, do you agree with what I said that the reason we take the real part is because once they are collinear and during division the imaginary part has no meaning?
|
|
|
|
Post by Admin on Sept 25, 2023 19:59:02 GMT
Ok, and you were right when you said the angle is staring at you - no matter where the vectors are in the plane (not starting from the origin) the angle between them is always the same. So in this case, no calculation is needed to see it is $\gamma$. But what abut the real part, do you agree with what I said that the reason we take the real part is because once they are collinear and during division the imaginary part has no meaning? Mondo No I definitely do not agree. The left hand side of the last equation on page 559 is a real quantity the second term is therefore also real. Vasco |
|
|
|
Post by mondo on Sept 26, 2023 5:49:35 GMT
This is not the explanation. I can see that the left hand side is a real quantity and therefore the division of a vector should also be. The question is rather why $\frac{|z+a|\cos(\gamma)}{|z-a|} = Re(\frac{z+a}{z-a})$, why the left hand side is a real part of this quotient on the right. This is what I don't quite understand. At first I thought it has to do with the fact these vector are collinear.
|
|
|
|
Post by mondo on Sept 26, 2023 6:04:23 GMT
Well it must be this! Imagine moving both of them to the origin, then we cast $z+a$ onto $z-a$ (or the other way around) but in book we do it by multiplying the first one by $\cos(\gamma)$. So now we have them collinear. Next imagine we rotate them clockwise until they are aligned with real axis, now a big question - what is theirs modulus/length? It is a real part $Re()$. Done.
|
|